Article contents
MONADIC INTUITIONISTIC AND MODAL LOGICS ADMITTING PROVABILITY INTERPRETATIONS
Published online by Cambridge University Press: 02 December 2021
Abstract
The Gödel translation provides an embedding of the intuitionistic logic
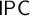 $\mathsf {IPC}$
into the modal logic
$\mathsf {IPC}$
into the modal logic
 $\mathsf {Grz}$
, which then embeds into the modal logic
$\mathsf {Grz}$
, which then embeds into the modal logic
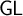 $\mathsf {GL}$
via the splitting translation. Combined with Solovay’s theorem that
$\mathsf {GL}$
via the splitting translation. Combined with Solovay’s theorem that
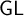 $\mathsf {GL}$
is the modal logic of the provability predicate of Peano Arithmetic
$\mathsf {GL}$
is the modal logic of the provability predicate of Peano Arithmetic
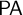 $\mathsf {PA}$
, both
$\mathsf {PA}$
, both
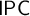 $\mathsf {IPC}$
and
$\mathsf {IPC}$
and
 $\mathsf {Grz}$
admit provability interpretations. When attempting to ‘lift’ these results to the monadic extensions
$\mathsf {Grz}$
admit provability interpretations. When attempting to ‘lift’ these results to the monadic extensions
 $\mathsf {MIPC}$
,
$\mathsf {MIPC}$
,
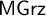 $\mathsf {MGrz}$
, and
$\mathsf {MGrz}$
, and
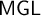 $\mathsf {MGL}$
of these logics, the same techniques no longer work. Following a conjecture made by Esakia, we add an appropriate version of Casari’s formula to these monadic extensions (denoted by a ‘+’), obtaining that the Gödel translation embeds
$\mathsf {MGL}$
of these logics, the same techniques no longer work. Following a conjecture made by Esakia, we add an appropriate version of Casari’s formula to these monadic extensions (denoted by a ‘+’), obtaining that the Gödel translation embeds
 $\mathsf {M^{+}IPC}$
into
$\mathsf {M^{+}IPC}$
into
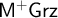 $\mathsf {M^{+}Grz}$
and the splitting translation embeds
$\mathsf {M^{+}Grz}$
and the splitting translation embeds
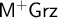 $\mathsf {M^{+}Grz}$
into
$\mathsf {M^{+}Grz}$
into
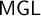 $\mathsf {MGL}$
. As proven by Japaridze, Solovay’s result extends to the monadic system
$\mathsf {MGL}$
. As proven by Japaridze, Solovay’s result extends to the monadic system
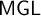 $\mathsf {MGL}$
, which leads us to a provability interpretation of both
$\mathsf {MGL}$
, which leads us to a provability interpretation of both
 $\mathsf {M^{+}IPC}$
and
$\mathsf {M^{+}IPC}$
and
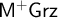 $\mathsf {M^{+}Grz}$
.
$\mathsf {M^{+}Grz}$
.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by



