Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-05-03T03:59:53.491Z Has data issue: false hasContentIssue false
  • English
  • Français

Vanishing theorem for tame harmonic bundles via L2-cohomology

Part of: (Co)homology theory Holomorphic fiber spaces Cycles and subschemes Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  03 April 2025

Ya Deng Open the ORCID record for Ya Deng [Opens in a new window]  and
Feng Hao
Ya Deng
Affiliation:
CNRS, Institut Élie Cartan de Lorraine, Université de Lorraine, Site de Nancy, 54506 Vandœuvre-lès-Nancy, France [email protected]
Feng Hao
Affiliation:
School of Mathematics, Shandong University, 27 Shanda South Road, Jinan 250100, PR China [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using 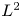$L^2$-methods, we prove a vanishing theorem for tame harmonic bundles over quasi-compact Kähler manifolds in a very general setting. As a special case, we give a completely new proof of the Kodaira-type vanishing theorems for Higgs bundles due to Arapura. To prove our vanishing theorem, we construct a fine resolution of the Dolbeault complex for tame harmonic bundles via the complex of sheaves of 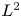$L^2$-forms, and we establish the Hörmander 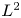$L^2$-estimate and solve 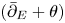$(\bar {\partial }_E+\theta )$-equations for Higgs bundles $(E,\theta )$.

Keywords

tame harmonic bundle(parabolic) Higgs bundlevanishing theoremHörmander L2-estimateBochner techniqueL2-cohomologySimpson–Mochizuki correspondence

MSC classification

Primary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture
Secondary: 14F17: Vanishing theorems 32L20: Vanishing theorems 14J60: Vector bundles on surfaces and higher-dimensional varieties, and their moduli
Type
Research Article
Information
Compositio Mathematica , Volume 160 , Issue 12 , December 2024 , pp. 2828 - 2855
Check for updates
Copyright
© The Author(s), 2025. The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andreotti, A. and Vesentini, E., Carleman estimates for the Laplace-Beltrami equation on complex manifolds, Inst. Hautes Études Sci. Publ. Math. 25 (1965), 81–130.CrossRefGoogle Scholar
Arapura, D., Kodaira-Saito vanishing via Higgs bundles in positive characteristic, J. Reine Angew. Math. 755 (2019), 293–312.CrossRefGoogle Scholar
Arapura, D., Hao, F. and Li, H., Vanishing theorems for parabolic Higgs bundles, Math. Res. Lett. 26 (2019), 1251–1279.CrossRefGoogle Scholar
Borne, N. and Vistoli, A., Parabolic sheaves on logarithmic schemes, Adv. Math. 231 (2012), 1327–1363.CrossRefGoogle Scholar
Cattani, E., Kaplan, A. and Schmid, W., Degeneration of Hodge structures, Ann. of Math. (2) 123 (1986), 457–535.CrossRefGoogle Scholar
Cattani, E., Kaplan, A. and Schmid, W., $L^2$ and intersection cohomologies for a polarizable variation of Hodge structure, Invent. Math. 87 (1987), 217–252.CrossRefGoogle Scholar
Deligne, P. and Illusie, L., Relèvements modulo $p^2$ et décomposition du complexe de de Rham, Invent. Math. 89 (1987), 247–270.CrossRefGoogle Scholar
Demailly, J.-P., Estimations $L^{2}$ pour l'opérateur $\bar \partial$ d'un fibré vectoriel holomorphe semi-positif au-dessus d'une variété kählérienne complète, Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 457–511.CrossRefGoogle Scholar
Demailly, J.-P., Complex Analytic and Differential Geometry (online book, 2012).Google Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Pseudo-effective line bundles on compact Kähler manifolds, Int. J. Math. 12 (2001), 689–741.CrossRefGoogle Scholar
Huang, C., Liu, K., Wan, X. and Yang, X., Vanishing theorems for sheaves of logarithmic differential forms on compact Kähler manifolds, Int. Math. Res. Not. IMRN 16 (2023), 13501–13523.CrossRefGoogle Scholar
Iyer, J. N. N. and Simpson, C. T., A relation between the parabolic Chern characters of the de Rham bundles, Math. Ann. 338 (2007), 347–383.CrossRefGoogle Scholar
Jost, J., Yang, Y.-H. and Zuo, K., The cohomology of a variation of polarized Hodge structures over a quasi-compact Kähler manifold, J. Algebraic Geom. 16 (2007), 401–434.CrossRefGoogle Scholar
Kashiwara, M., The asymptotic behavior of a variation of polarized Hodge structure, Publ. Res. Inst. Math. Sci. 21 (1985), 853–875.CrossRefGoogle Scholar
Kashiwara, M. and Kawai, T., The Poincaré lemma for variations of polarized Hodge structure, Publ. Res. Inst. Math. Sci. 23 (1987), 345–407.CrossRefGoogle Scholar
Lan, G., Sheng, M., Yang, Y. and Zuo, K., Semistable Higgs bundles of small ranks are strongly Higgs semistable, Preprint (2013), arXiv:1311.2405.Google Scholar
Lan, G., Sheng, M. and Zuo, K., Semistable Higgs bundles, periodic Higgs bundles and representations of algebraic fundamental groups, J. Eur. Math. Soc. (JEMS) 21 (2019), 3053–3112.CrossRefGoogle Scholar
Langer, A., Bogomolov's inequality for Higgs sheaves in positive characteristic, Invent. Math. 199 (2015), 889–920.CrossRefGoogle Scholar
Maruyama, M. and Yokogawa, K., Moduli of parabolic stable sheaves, Math. Ann. 293 (1992), 77–99.CrossRefGoogle Scholar
Mochizuki, T., Asymptotic behaviour of tame nilpotent harmonic bundles with trivial parabolic structure, J. Differential Geom. 62 (2002), 351–559.CrossRefGoogle Scholar
Mochizuki, T., Kobayashi–Hitchin correspondence for tame harmonic bundles and an application, Astérisque 309 (2006).Google Scholar
Mochizuki, T., Asymptotic behaviour of tame harmonic bundles and an application to pure twistor $D$-modules, part 1, Mem. Amer. Math. Soc. 185 (2007), 869.Google Scholar
Popa, M., Kodaira-Saito vanishing and applications, Enseign. Math. 62 (2016), 49–89.CrossRefGoogle Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.CrossRefGoogle Scholar
Shiffman, B. and Sommese, A. J., Vanishing theorems on complex manifolds, Progress in Mathematics, vol. 56 (Birkhäuser Boston, Boston, MA, 1985).CrossRefGoogle Scholar
Simpson, C. T., Constructing variations of Hodge structure using Yang-Mills theory and applications to uniformization, J. Amer. Math. Soc. 1 (1988), 867–918.CrossRefGoogle Scholar
Simpson, C. T., Harmonic bundles on noncompact curves, J. Amer. Math. Soc. 3 (1990), 713–770.CrossRefGoogle Scholar
Simpson, C. T., Higgs bundles and local systems, Inst. Hautes Études Sci. Publ. Math. 75 (1992), 5–95.CrossRefGoogle Scholar
Zucker, S., Hodge theory with degenerating coefficients. $L_{2}$ cohomology in the Poincaré metric, Ann. of Math. (2) 109 (1979), 415–476.CrossRefGoogle Scholar