Article contents
Limit theory for U-statistics under geometric and topological constraints with rare events
Published online by Cambridge University Press: 14 September 2022
Abstract
We study the geometric and topological features of U-statistics of order k when the k-tuples satisfying geometric and topological constraints do not occur frequently. Using appropriate scaling, we establish the convergence of U-statistics in vague topology, while the structure of a non-degenerate limit measure is also revealed. Our general result shows various limit theorems for geometric and topological statistics, including persistent Betti numbers of Čech complexes, the volume of simplices, a functional of the Morse critical points, and values of the min-type distance function. The required vague convergence can be obtained as a result of the limit theorem for point processes induced by U-statistics. The latter convergence particularly occurs in the
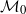 $\mathcal M_0$
-topology.
$\mathcal M_0$
-topology.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 2
- Cited by



