No CrossRef data available.
Article contents
Absence of singularities in solutions for the compressible Euler equations with source terms in $\mathbb {R}^d$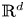
Published online by Cambridge University Press: 26 April 2022
Abstract
The present article is devoted to the study of global solution and large time behaviour of solution for the isentropic compressible Euler system with source terms in $\mathbb {R}^d$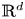 , $d\geq 1$
, $d\geq 1$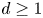 , which extends and improves the results obtained by Sideris et al. in ‘T.C. Sideris, B. Thomases, D.H. Wang, Long time behavior of solutions to the 3D compressible Euler equations with damping, Comm. Partial Differential Equations 28 (2003) 795–816’. We first establish the existence and uniqueness of global smooth solution provided the initial datum is sufficiently small, which tells us that the damping terms can prevent the development of singularity in small amplitude. Next, under the additional smallness assumption, the large time behaviour of solution is investigated, we only obtain the algebra decay of solution besides the $L^2$
, which extends and improves the results obtained by Sideris et al. in ‘T.C. Sideris, B. Thomases, D.H. Wang, Long time behavior of solutions to the 3D compressible Euler equations with damping, Comm. Partial Differential Equations 28 (2003) 795–816’. We first establish the existence and uniqueness of global smooth solution provided the initial datum is sufficiently small, which tells us that the damping terms can prevent the development of singularity in small amplitude. Next, under the additional smallness assumption, the large time behaviour of solution is investigated, we only obtain the algebra decay of solution besides the $L^2$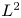 -norm of $\nabla u$
-norm of $\nabla u$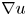 is exponential decay.
is exponential decay.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 978 - 1001
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh



