In this paper, we study the approximate minimization problem of weighted finite automata (WFAs): to compute the best possible approximation of a WFA given a bound on the number of states. By reformulating the problem in terms of Hankel matrices, we leverage classical results on the approximation of Hankel operators, namely the celebrated Adamyan-Arov-Krein (AAK) theory. We solve the optimal spectral-norm approximate minimization problem for irredundant WFAs with real weights, defined over a one-letter alphabet. We present a theoretical analysis based on AAK theory and bounds on the quality of the approximation in the spectral norm and 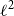$\ell ^2$ norm. Moreover, we provide a closed-form solution, and an algorithm, to compute the optimal approximation of a given size in polynomial time.

Real functions on the domain [0,1)n – often used to describe digital images – allow for different well-known types of binary operations. In this note, we recapitulate how weighted finite automata can be used in order to represent those functions and how certain binary operations are reflected in the theory of these automata. Different types of products of automata are employed, including the seldomly-used full Cartesian product. We show, however, the infeasibility of functional composition; simple examples yield that the class of automatic functions (i.e., functions computable by automata) is not closed under this operation.