We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This work deals with the study of some stratigraphic models for the formation of geological basins under a maximal erosion rate constrain. It leads to introduce differentialinclusions of degenerated hyperbolic-parabolic type $0\in \partial _{t}u-div\{H(\partial _{t}u+E)\nabla u\}$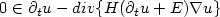 
, where H is the maximal monotonous graph of the Heaviside function and E is a given non-negative function. Firstly, we present the new and realistic models and an original mathematical formulation, taking into account the weather-limited rate constraint in the conservation law, with a unilateral constraint on the outflow boundary. Then, we give a study of the 1-D case with numerical illustrations.
