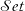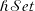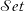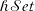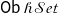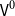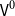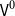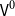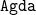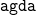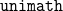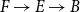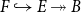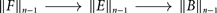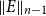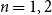When working in homotopy type theory and univalent foundations, the traditional role of the category of sets, 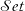 $\mathcal{Set}$, is replaced by the category
$\mathcal{Set}$, is replaced by the category 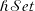 $\mathcal{hSet}$ of homotopy sets (h-sets); types with h-propositional identity types. Many of the properties of
$\mathcal{hSet}$ of homotopy sets (h-sets); types with h-propositional identity types. Many of the properties of 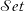 $\mathcal{Set}$ hold for
$\mathcal{Set}$ hold for 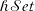 $\mathcal{hSet}$ ((co)completeness, exactness, local cartesian closure, etc.). Notably, however, the univalence axiom implies that
$\mathcal{hSet}$ ((co)completeness, exactness, local cartesian closure, etc.). Notably, however, the univalence axiom implies that 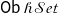 $\mathsf{Ob}\,\mathcal{hSet}$ is not itself an h-set, but an h-groupoid. This is expected in univalent foundations, but it is sometimes useful to also have a stricter universe of sets, for example, when constructing internal models of type theory. In this work, we equip the type of iterative sets
$\mathsf{Ob}\,\mathcal{hSet}$ is not itself an h-set, but an h-groupoid. This is expected in univalent foundations, but it is sometimes useful to also have a stricter universe of sets, for example, when constructing internal models of type theory. In this work, we equip the type of iterative sets 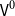 $\mathsf{V}^0$, due to Gylterud ((2018). The Journal of Symbolic Logic 83 (3) 1132–1146) as a refinement of the pioneering work of Aczel ((1978). Logic Colloquium’77, Studies in Logic and the Foundations of Mathematics, vol. 96, Elsevier, 55–66.) on universes of sets in type theory, with the structure of a Tarski universe and show that it satisfies many of the good properties of h-sets. In particular, we organize
$\mathsf{V}^0$, due to Gylterud ((2018). The Journal of Symbolic Logic 83 (3) 1132–1146) as a refinement of the pioneering work of Aczel ((1978). Logic Colloquium’77, Studies in Logic and the Foundations of Mathematics, vol. 96, Elsevier, 55–66.) on universes of sets in type theory, with the structure of a Tarski universe and show that it satisfies many of the good properties of h-sets. In particular, we organize 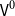 $\mathsf{V}^0$ into a (non-univalent strict) category and prove that it is locally cartesian closed. This enables us to organize it into a category with families with the structure necessary to model extensional type theory internally in HoTT/UF. We do this in a rather minimal univalent type theory with W-types, in particular we do not rely on any HITs, or other complex extensions of type theory. Furthermore, the construction of
$\mathsf{V}^0$ into a (non-univalent strict) category and prove that it is locally cartesian closed. This enables us to organize it into a category with families with the structure necessary to model extensional type theory internally in HoTT/UF. We do this in a rather minimal univalent type theory with W-types, in particular we do not rely on any HITs, or other complex extensions of type theory. Furthermore, the construction of 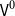 $\mathsf{V}^0$ and the model is fully constructive and predicative, while still being very convenient to work with as the decoding from
$\mathsf{V}^0$ and the model is fully constructive and predicative, while still being very convenient to work with as the decoding from 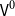 $\mathsf{V}^0$ into h-sets commutes definitionally for all type constructors. Almost all of the paper has been formalized in
$\mathsf{V}^0$ into h-sets commutes definitionally for all type constructors. Almost all of the paper has been formalized in 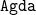 $\texttt{Agda}$ using the
$\texttt{Agda}$ using the 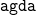 $\texttt{agda}$-
$\texttt{agda}$- $\texttt{unimath}$ library of univalent mathematics.
$\texttt{unimath}$ library of univalent mathematics.