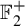1 results
Substreetutions and more on trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 2399-2453
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
We define a notion of substitution on colored binary trees that we call substreetution. We show that a point fixed by a substreetution may (or not) be almost periodic, and thus the closure of the orbit under the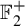
$\mathbb {F}_{2}^{+}$-action may (or not) be minimal. We study one special example: we show that it belongs to the minimal case and that the number of preimages in the minimal set increases just exponentially fast, whereas it could be expected a super-exponential growth. We also give examples of periodic trees without invariant measures on their orbit. We use our construction to get quasi-periodic colored tilings of the hyperbolic disk.
