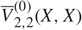In Weil (2001) formulae were proved for stationary Boolean models Z in ℝd with convex or polyconvex grains, which express the densities (specific mean values) of mixed volumes of Z in terms of related mean values of the underlying Poisson particle process X. These formulae were then used to show that in dimensions 2 and 3 the densities of mixed volumes of Z determine the intensity γ of X. For d = 4, a corresponding result was also stated, but the proof given was incomplete, since in the formula for the density of the Euler characteristic V̅0(Z) of Z a term 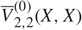 $\overline V^{(0)}_{2,2}(X,X)$ was missing. This was pointed out in Goodey and Weil (2002), where it was also explained that a new decomposition result for mixed volumes and mixed translative functionals would be needed to complete the proof. Such a general decomposition result has recently been proved by Hug, Rataj, and Weil (2013), (2018) and is based on flag measures of the convex bodies involved. Here, we show that such flag representations not only lead to a correct derivation of the four-dimensional result, but even yield a corresponding uniqueness theorem in all dimensions. In the proof of the latter we make use of Alesker’s representation theorem for translation invariant valuations. We also discuss which shape information can be obtained in this way and comment on the situation in the nonstationary case.
$\overline V^{(0)}_{2,2}(X,X)$ was missing. This was pointed out in Goodey and Weil (2002), where it was also explained that a new decomposition result for mixed volumes and mixed translative functionals would be needed to complete the proof. Such a general decomposition result has recently been proved by Hug, Rataj, and Weil (2013), (2018) and is based on flag measures of the convex bodies involved. Here, we show that such flag representations not only lead to a correct derivation of the four-dimensional result, but even yield a corresponding uniqueness theorem in all dimensions. In the proof of the latter we make use of Alesker’s representation theorem for translation invariant valuations. We also discuss which shape information can be obtained in this way and comment on the situation in the nonstationary case.