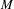1 results
II1 FACTORS WITH EXOTIC CENTRAL SEQUENCE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 19 December 2019, pp. 1671-1696
- Print publication:
- September 2021
-
- Article
- Export citation