The problem of synchronizing a network
of identical processors that work synchronously
at discrete steps is studied. Processors are arranged as an array of
m rows and n columns and can exchange each other only one bit
of information.
We give algorithms which
synchronize square arrays of (n × n) processors and give some
general constructions to synchronize arrays of (m × n) processors.
Algorithms are given to synchronize in time n2, $n \lceil \log n\rceil$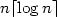 ,
$n\lceil\sqrt n \rceil$
,
$n\lceil\sqrt n \rceil$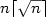 and 2n a square array of (n × n) processors.
Our approach is a modular description of
synchronizing algorithms in terms of "fragments" of cellular automata that are
called
signals.
Compositional rules to obtain new signals (and new synchronization
times) starting from known ones are given for an (m × n) array.
Using these compositional rules we construct
synchronizations in any "feasible" linear time and in any time expressed
by a polynomial with nonnegative coefficients.
and 2n a square array of (n × n) processors.
Our approach is a modular description of
synchronizing algorithms in terms of "fragments" of cellular automata that are
called
signals.
Compositional rules to obtain new signals (and new synchronization
times) starting from known ones are given for an (m × n) array.
Using these compositional rules we construct
synchronizations in any "feasible" linear time and in any time expressed
by a polynomial with nonnegative coefficients.