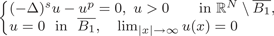1 results
Fast and slow decay solutions for supercritical fractional elliptic problems in exterior domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 28-53
- Print publication:
- February 2022
-
- Article
- Export citation
-
We consider the fractional elliptic problem:
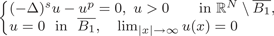where B1 is the unit ball in ℝN, N ⩾ 3, s ∈ (0, 1) and p > (N + 2s)/(N − 2s). We prove that this problem has infinitely many solutions with slow decay O(|x|−2s/(p−1)) at infinity. In addition, for each s ∈ (0, 1) there exists Ps > (N + 2s)/(N − 2s), for any (N + 2s)/(N − 2s) < p < Ps, the above problem has a solution with fast decay O(|x|2s−N). This result is the extension of the work by Dávila, del Pino, Musso and Wei (2008, Calc. Var. Partial Differ. Equ. 32, no. 4, 453–480) to the fractional case.
