We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
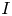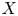The paper alluded to in the title contains the following striking result: Let I be the unit interval and \Delta the Cantor set. If X is a quasi Banach space containing no copy of c_{0} 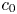which is isomorphic to a closed subspace of a space with a basis and C(I,\,X) 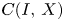is linearly homeomorphic to C(\Delta ,\, X)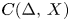, then X 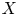is locally convex, i.e., a Banach space. We will show that Kalton result is sharp by exhibiting non-locally convex quasi Banach spaces X 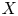with a basis for which C(I,\,X) 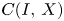and C(\Delta ,\, X) 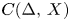are isomorphic. Our examples are rather specific and actually, in all cases, X 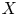is isomorphic to C(K,\,X) 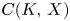if K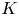 is a metric compactum of finite covering dimension.
Email your librarian or administrator to recommend adding this to your organisation's collection.
