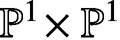1 results
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
- Print publication:
- June 2021
-
- Article
- Export citation