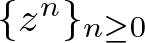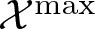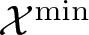Motivated by new examples of functional Banach spaces over the unit disk, arising as the symbol spaces in the study of random analytic functions, for which the monomials 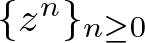 $\{z^n\}_{n\geq 0}$ exhibit features of an unconditional basis yet they often don’t even form a Schauder basis, we introduce a notion called solid basis for Banach spaces and p-Banach spaces and study its properties. Besides justifying the rich existence of solid bases, we study their relationship with unconditional bases, the weak-star convergence of Taylor polynomials, the problem of a solid span and the curious roles played by c0. The two features of this work are as follows: (1) during the process, we are led to revisit the axioms satisfied by a typical Banach space of analytic functions over the unit disk, leading to a notion of
$\{z^n\}_{n\geq 0}$ exhibit features of an unconditional basis yet they often don’t even form a Schauder basis, we introduce a notion called solid basis for Banach spaces and p-Banach spaces and study its properties. Besides justifying the rich existence of solid bases, we study their relationship with unconditional bases, the weak-star convergence of Taylor polynomials, the problem of a solid span and the curious roles played by c0. The two features of this work are as follows: (1) during the process, we are led to revisit the axioms satisfied by a typical Banach space of analytic functions over the unit disk, leading to a notion of 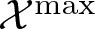 $\mathcal{X}^\mathrm{max}$ (and
$\mathcal{X}^\mathrm{max}$ (and 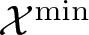 $\mathcal{X}^\mathrm{min}$), as well as a number of related functorial constructions, which are of independent interests; (2) the main interests of solid basis lie in the case of non-separable (p-)Banach spaces, such as BMOA and the Bloch space instead of VMOA and the little Bloch space.
$\mathcal{X}^\mathrm{min}$), as well as a number of related functorial constructions, which are of independent interests; (2) the main interests of solid basis lie in the case of non-separable (p-)Banach spaces, such as BMOA and the Bloch space instead of VMOA and the little Bloch space.