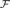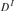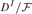Criteria are obtained for a filter 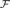${\cal F}$ of subsets of a set I to be an intersection of finitely many ultrafilters, respectively, finitely many κ-complete ultrafilters for a given uncountable cardinal $\kappa .$ From these, general results are deduced concerning homomorphisms on infinite direct product groups, which yield quick proofs of some results in the literature: the Łoś–Eda theorem (characterizing homomorphisms from a not-necessarily-countable direct product of modules to a slender module), and some results of Nahlus and the author on homomorphisms on infinite direct products of not-necessarily-associative k-algebras. The same tools allow other results of Nahlus and the author to be nontrivially strengthened, and yield an analog to one of their results, with nonabelian groups taking the place of k-algebras.

We briefly examine the question of how the common technique used in applying the general results of this note to k-algebras on the one hand, and to nonabelian groups on the other, might be extended to more general varieties of algebras in the sense of universal algebra.

In a final section, the Erdős–Kaplansky theorem on dimensions of vector spaces 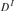${D^I}$$(D$ a division ring) is extended to reduced products 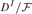${D^I}/{\cal F},$ and an application is noted.