We consider the shift-invariant space, 𝕊(Φ), generated by a set Φ = {Φ1,..., Φr} of compactly supported distributions on R when the vector of distributions ϕ:= {Φ1,..., Φr} T satisfies a system of refinement equations expressed in matrix form as

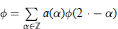
where a is a finitely supported sequence of r x r matrices of complex numbers. Such multiple refinable functions occur naturally in the study of multiple wavelets.

The purpose of the present paper is to characterize the accuracy of Φ, the order of the polynomial space contained in 𝕊(Φ), strictly in terms of the refinement mask a. The accuracy determines the Lp-approximation order of 𝕊(Φ) when the functions in (Φ) belong to Lp(ℝ) (see Jia [10]). The characterization is achieved in terms of the eigenvalues and eigenvectors of the subdivision operator associated with the mask a. In particular, they extend and improve the results of Heil, Strang and Strela [7], and of Plonka [16]. In addition, a counterexample is given to the statement of Strang and Strela [20] that the eigenvalues of the subdivision operator determine the accuracy. The results do not require the linear independence of the shifts of Φ.