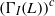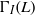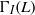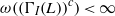2 results
ON WEAKLY PERFECT ANNIHILATING-IDEAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 11 May 2021, pp. 362-372
- Print publication:
- December 2021
-
- Article
- Export citation
COMPLEMENT OF THE ZERO DIVISOR GRAPH OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 June 2013, pp. 177-190
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation