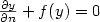We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This paper is concerned with the global exact controllability ofthe semilinear heat equation (with nonlinear terms involving the state andthe gradient) completed with boundary conditions of the form ${\partialy\over\partial n} + f(y) = 0$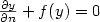 
. We consider distributed controls, with support in a small set. The null controllability of similar linear systems has been analyzedin a previous first part of this work. In this second part we show that, when the nonlinear terms arelocally Lipschitz-continuous and slightly superlinear, one has exactcontrollability to the trajectories.
