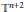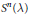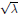2 results
Semiclassical Limits of Eigenfunctions on Flat n-Dimensional Tori
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-12
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
Semiclassical Limits of Heat Kernels of Laplacians on theh-Heisenberg Group
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 132-142
- Print publication:
- 2013
-
- Article
- Export citation