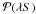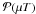In many applications, we assume that two random observations x andy are generated according to independent Poisson distributions\hbox{$\PPP(\lambdaS)$}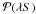𝒫(λS)and \hbox{$\PPP(\muT)$}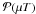𝒫(μT)and we are interested in performing statistical inference on the ratioφ = λ / μ of the twoincidence rates. In vaccine efficacy trials, x and y aretypically the numbers of cases in the vaccine and the control groups respectively,φ is called the relative risk and the statistical model is called‘partial immunity model’. In this paper we start by defining a natural semi-conjugatefamily of prior distributions for this model, allowing straightforward computation of theposterior inference. Following theory on reference priors, we define the reference priorfor the partial immunity model when φ is the parameter of interest. Wealso define a family of reference priors with partial information on μwhile remaining uninformative about φ. We notice that these priors belongto the semi-conjugate family. We then demonstrate using numerical examples that Bayesiancredible intervals for φ enjoy attractive frequentist properties whenusing reference priors, a typical property of reference priors.