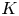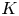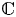We prove the strong Suslin reciprocity law conjectured by A. Goncharov. The Suslin reciprocity law is a generalization of the Weil reciprocity law to higher Milnor $K$-theory. The Milnor $K$-groups can be identified with the top cohomology groups of the polylogarithmic motivic complexes; Goncharov's conjecture predicts the existence of a contracting homotopy underlying Suslin reciprocity. The main ingredient of the proof is a homotopy invariance theorem for the cohomology of the polylogarithmic motivic complexes in the ‘next to Milnor’ degree. We apply these results to the theory of scissors congruences of hyperbolic polytopes. For every triple of rational functions on a compact projective curve over $\mathbb {C}$ we construct a hyperbolic polytope (defined up to scissors congruence). The hyperbolic volume and the Dehn invariant of this polytope can be computed directly from the triple of rational functions on the curve.

For compact hyperbolic 3-manifolds we lift the Bloch invariant defined by Neumann and Yang to an integral class in K3(ℂ). Applying the Borel and the Bloch regulators, one gets back the volume and the Chern-Simons invariant of the manifold. We perform our constructions in stable homotopy theory, pushing a generalized orientation of the manifold directly into K-theory. On the way we give a purely homotopical construction of the Bloch-Wigner exact sequence which allows us to explain the ℚ/ℤ ambiguity that appears in the non-compact case.