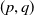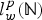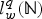3 results
On a weighted anisotropic eigenvalue problem
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 October 2024, pp. 72-85
- Print publication:
- January 2025
-
- Article
-
- You have access
- HTML
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation
A note on the regularity of solutionsof Hamilton-Jacobi equations with superlinear growthin the gradient variable
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 15 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 28 March 2008, pp. 367-376
- Print publication:
- April 2009
-
- Article
- Export citation