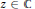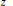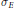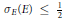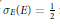Potential Theory of the Farthest-Point Distance Function
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 3 / 01 September 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 373-387
- Print publication:
- 01 September 2003
-
- Article
-
- You have access
- Export citation
-
We study the farthest-point distance function, which measures the distance from 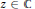z\,\in \,\mathbb{C} to the farthest point or points of a given compact set E in the plane.
The logarithm of this distance is subharmonic as a function of 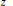z, and equals the logarithmic potential of a unique probability measure with unbounded support. This measure 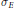{{\sigma }_{E}} has many interesting properties that reflect the topology and geometry of the compact set E. We prove 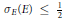{{\sigma }_{E}}(E)\,\le \,\frac{1}{2} for polygons inscribed in a circle, with equality if and only if E is a regular n-gon for some odd n. Also we show 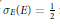{{\sigma }_{E}}(E)\,=\,\frac{1}{2} for smooth convex sets of constant width. We conjecture 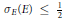{{\sigma }_{E}}(E)\,\le \,\frac{1}{2} for all E.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
