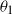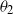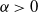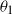In addition to the features of the two-parameter Chinese restaurant process (CRP), the restaurant under consideration has a cocktail bar and hence allows for a wider range of (bar and table) occupancy mechanisms. The model depends on three real parameters, $\alpha$ , $\theta_1$ , and 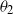$\theta_2$ , fulfilling certain conditions. Results known for the two-parameter CRP are carried over to this model. We study the number of customers at the cocktail bar, the number of customers at each table, and the number of occupied tables after n customers have entered the restaurant. For 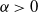$\alpha>0$ the number of occupied tables, properly scaled, is asymptotically three-parameter Mittag–Leffler distributed as n tends to infinity. We provide representations for the two- and three-parameter Mittag–Leffler distribution leading to efficient random number generators for these distributions. The proofs draw heavily from methods known for exchangeable random partitions, martingale methods known for generalized Pólya urns, and results known for the two-parameter CRP.

An algorithm is developed for exact simulation from distributions that are defined as fixed points of maps between spaces of probability measures. The fixed points of the class of maps under consideration include examples of limit distributions of random variables studied in the probabilistic analysis of algorithms. Approximating sequences for the densities of the fixed points with explicit error bounds are constructed. The sampling algorithm relies on a modified rejection method.