1 results
Probabilistic interpretation and random walkon spheres algorithms for the Poisson-Boltzmann equationin molecular dynamics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 44 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 26 August 2010, pp. 997-1048
- Print publication:
- September 2010
-
- Article
- Export citation
-
Motivated by the development of efficient Monte Carlo methodsfor PDE models in molecular dynamics,we establish a new probabilistic interpretation of a family of divergence formoperators with discontinuous coefficients at the interfaceof two open subsets of $\mathbb{R}^d$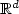
. This family of operators includes the case of thelinearized Poisson-Boltzmann equation used tocompute the electrostatic free energy of a molecule.More precisely, we explicitly construct a Markov process whoseinfinitesimal generator belongs to this family, as the solution of a SDEincluding a non standard local time term related to the interfaceof discontinuity. We then prove an extendedFeynman-Kac formula for the Poisson-Boltzmann equation.This formula allows us to justifyvarious probabilistic numerical methods toapproximate the free energy of a molecule.We analyse the convergence rate of these simulation procedures andnumerically compare them on idealized molecules models.
