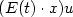Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

quantum control.

ESAIM: Control, Optimisation and Calculus of Variations (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

Limitations on the control of Schrödinger equations
Reinhard Illner, Horst Lange, Holger Teismann
Journal:

ESAIM: Control, Optimisation and Calculus of Variations / Volume 12 / Issue 4 / October 2006

Published online by Cambridge University Press:

11 October 2006, pp. 615-635

Print publication:

October 2006
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We give the definitions of exact and approximate controllability forlinear and nonlinear Schrödinger equations, review fundamental criteria for controllability and revisit a classical “No-go” resultfor evolution equations due to Ball, Marsden and Slemrod. In Section 2 we prove corresponding results on non-controllabilityfor the linear Schrödinger equation and distributed additive control,and we show that the Hartree equation of quantum chemistry with bilinearcontrol $(E(t)\cdot x) u$ 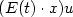is not controllable in finite or infinite time. Finally, in Section 3, we give criteria for additive controllability of linear Schrödinger equations, andwe give a distributed additive controllability result for the nonlinear Schrödinger equation if the data are small.