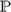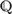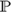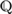1 results
QUANTIFIED INTUITIONISTIC LOGIC OVER METRIZABLE SPACES
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 08 April 2019, pp. 405-425
- Print publication:
- September 2019
-
- Article
- Export citation
-
In the topological semantics, quantified intuitionistic logic, QH, is known to be strongly complete not only for the class of all topological spaces but also for some particular topological spaces — for example, for the irrational line,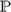
${\Bbb P}$, and for the rational line, 
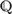${\Bbb Q}$, in each case with a constant countable domain for the quantifiers. Each of 
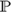${\Bbb P}$ and 
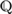${\Bbb Q}$ is a separable zero-dimensional dense-in-itself metrizable space. The main result of the current article generalizes these known results: QH is strongly complete for any zero-dimensional dense-in-itself metrizable space with a constant domain of cardinality ≤ the space’s weight; consequently, QH is strongly complete for any separable zero-dimensional dense-in-itself metrizable space with a constant countable domain. We also prove a result that follows from earlier work of Moerdijk: if we allow varying domains for the quantifiers, then QH is strongly complete for any dense-in-itself metrizable space with countable domains.
