1 results
Lower bounds to the size of constant-depth propositional proofs
-
- Journal:
- The Journal of Symbolic Logic / Volume 59 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-86
- Print publication:
- March 1994
-
- Article
- Export citation

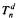 of depth
of depth 