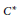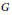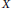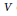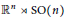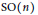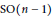We investigate the representation theory of the crossed-product ${{C}^{*}}$-algebra associated with a compact group $G$ acting on a locally compact space $X$ when the stability subgroups vary discontinuously. Our main result applies when $G$ has a principal stability subgroup or $X$ is locally of finite $G$-orbit type. Then the upper multiplicity of the representation of the crossed product induced from an irreducible representation $V$ of a stability subgroup is obtained by restricting $V$ to a certain closed subgroup of the stability subgroup and taking the maximum of the multiplicities of the irreducible summands occurring in the restriction of $V$. As a corollary we obtain that when the trivial subgroup is a principal stability subgroup; the crossed product is a Fell algebra if and only if every stability subgroup is abelian. A second corollary is that the ${{C}^{*}}$-algebra of the motion group ${{\mathbb{R}}^{n}}\,\rtimes \,\text{SO}\left( n \right)$ is a Fell algebra. This uses the classical branching theorem for the special orthogonal group $\text{SO}\left( n \right)$ with respect to $\text{SO}\left( n-1 \right)$. Since proper transformation groups are locally induced from the actions of compact groups, we describe how some of our results can be extended to transformation groups that are locally proper.

Let $G$ be a Lie groupoid over $M$ such that the target-source map from $G$ to $M\times M$ is proper. We show that, if $\mathcal{O}$ is an orbit of finite type (i.e. which admits a proper function with finitely many critical points), then the restriction $G|_\mathcal{U}$ of $G$ to some neighbourhood $\mathcal{U}$ of $\mathcal{O}$ in $M$ is isomorphic to a similar restriction of the action groupoid for the linear action of the transitive groupoid $G|_\mathcal{O}$ on the normal bundle $N\mathcal{O}$. The proof uses a deformation argument based on a cohomology vanishing theorem, along with a slice theorem which is derived from a new result on submersions with a fibre of finite type.

AMS 2000 Mathematics subject classification: Primary 58H05. Secondary 57R99

We present a new approach to singular reduction of Hamiltonian systems with symmetries. The tools we use are the category of differential spaces of Sikorski and the Stefan-Sussmann theorem. The former is applied to analyze the differential structure of the spaces involved and the latter is used to prove that some of these spaces are smooth manifolds.

Our main result is the identification of accessible sets of the generalized distribution spanned by the Hamiltonian vector fields of invariant functions with singular reduced spaces. We are also able to describe the differential structure of a singular reduced space corresponding to a coadjoint orbit which need not be locally closed.