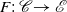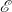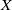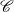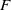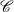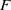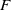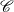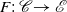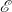Let $F:\; {\mathscr {C}} \to {\mathscr {E}} \ $ be a functor from a category $\mathscr {C} \ $ to a homological (Borceux–Bourn) or semi-abelian (Janelidze–Márki–Tholen) category $\mathscr {E}$. We investigate conditions under which the homology of an object 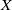$X$ in 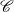$\mathscr {C}$ with coefficients in the functor 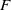$F$, defined via projective resolutions in 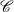$\mathscr {C}$, remains independent of the chosen resolution. Consequently, the left derived functors of 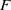$F$ can be constructed analogously to the classical abelian case.

Our approach extends the concept of chain homotopy to a non-additive setting using the technique of imaginary morphisms. Specifically, we utilize the approximate subtractions of Bourn–Janelidze, originally introduced in the context of subtractive categories. This method is applicable when $\mathscr {C}$ is a pointed regular category with finite coproducts and enough projectives, provided the class of projectives is closed under protosplit subobjects, a new condition introduced in this article and naturally satisfied in the abelian context. We further assume that the functor 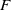$F$ meets certain exactness conditions: for instance, it may be protoadditive and preserve proper morphisms and binary coproducts—conditions that amount to additivity when 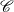$\mathscr {C}$ and $\mathscr {E}$ are abelian categories.

Within this framework, we develop a basic theory of derived functors, compare it with the simplicial approach, and provide several examples.