1 results
Symbolic dynamics for pointwise hyperbolic systems on open regions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 10 September 2024, pp. 1-54
-
- Article
-
- You have access
- HTML
- Export citation
-
Under certain conditions, we construct a countable Markov partition for pointwise hyperbolic diffeomorphism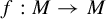
$f:M\rightarrow M$ on an open invariant subset 
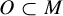$O\subset M$, which allows the Lyapunov exponents to be zero. From this partition, we define a symbolic extension that is finite-to-one and onto a subset of O that carries the same finite f-invariant measures as O. Our method relies upon shadowing theory of a recurrent-pointwise-pseudo-orbit that we introduce. As a canonical application, we estimate the number of closed orbits for f.
