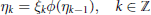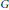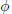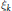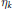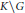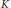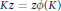We consider the stochastic difference equation 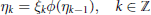{{\eta }_{k}}\,=\,{{\xi }_{k}}\phi \left( {{\eta }_{k-1}} \right),\,\,k\,\in \,\mathbb{Z}${{\eta }_{k}}\,=\,{{\xi }_{k}}\phi \left( {{\eta }_{k-1}} \right),\,\,k\,\in \,\mathbb{Z}$ on a locally compact group 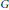G$G$, where 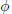\phi $\phi$ is an automorphism of 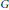G$G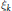$, {{\xi }_{K}}${{\xi }_{K}}$ are given 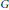G$G$-valued random variables, and 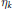{{\eta }_{k}}${{\eta }_{k}}$ are unknown 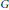G$G$-valued random variables. This equation was considered by Tsirelson and Yor on a one-dimensional torus. 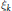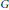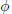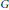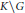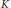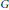We consider the case when {{\xi }_{K}}${{\xi }_{K}}$ have a common law \mu $\mu$ and prove that if G$G$ is a distal group and \phi $\phi$ is a distal automorphism of G$G$ and if the equation has a solution, then extremal solutions of the equation are in one-to-one correspondence with points on the coset space K\backslash G$K\backslash G$ for some compact subgroup K$K$ of G$G$ such that \mu $\mu$ is supported on 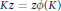Kz\,=\,z\phi \left( K \right)$Kz\,=\,z\phi \left( K \right)$ for any z$z$ in the support of \mu $\mu$. We also provide a necessary and sufficient condition for the existence of solutions to the equation.