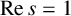1 results
BOUNDING ZETA ON THE 1-LINE UNDER THE PARTIAL RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 10 January 2024, pp. 244-251
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation