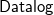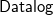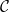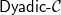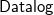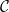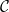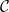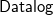Existential rules form an expressive 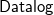 ${{\textsf{Datalog}}}$-based language to specify ontological knowledge. The presence of existential quantification in rule-heads, however, makes the main reasoning tasks undecidable. To overcome this limitation, in the last two decades, a number of classes of existential rules guaranteeing the decidability of query answering have been proposed. Unfortunately, only some of these classes fully encompass
${{\textsf{Datalog}}}$-based language to specify ontological knowledge. The presence of existential quantification in rule-heads, however, makes the main reasoning tasks undecidable. To overcome this limitation, in the last two decades, a number of classes of existential rules guaranteeing the decidability of query answering have been proposed. Unfortunately, only some of these classes fully encompass 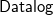 ${{\textsf{Datalog}}}$ and, often, this comes at the price of higher computational complexity. Moreover, expressive classes are typically unable to exploit tools developed for classes exhibiting lower expressiveness. To mitigate these shortcomings, this paper introduces a novel general syntactic condition that allows us to define, systematically and in a uniform way, from any decidable class
${{\textsf{Datalog}}}$ and, often, this comes at the price of higher computational complexity. Moreover, expressive classes are typically unable to exploit tools developed for classes exhibiting lower expressiveness. To mitigate these shortcomings, this paper introduces a novel general syntactic condition that allows us to define, systematically and in a uniform way, from any decidable class 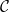 $\mathcal{C}$ of existential rules, a new class called
$\mathcal{C}$ of existential rules, a new class called 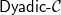 ${{\textsf{Dyadic-}\mathcal{C}}}$ enjoying the following properties: (i) it is decidable; (ii) it generalizes
${{\textsf{Dyadic-}\mathcal{C}}}$ enjoying the following properties: (i) it is decidable; (ii) it generalizes 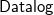 ${{\textsf{Datalog}}}$; (iii) it generalizes
${{\textsf{Datalog}}}$; (iii) it generalizes 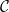 $\mathcal{C}$; (iv) it can effectively exploit any reasoner for query answering over
$\mathcal{C}$; (iv) it can effectively exploit any reasoner for query answering over 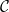 $\mathcal{C}$; and (v) its computational complexity does not exceed the highest between the one of
$\mathcal{C}$; and (v) its computational complexity does not exceed the highest between the one of 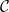 $\mathcal{C}$ and the one of
$\mathcal{C}$ and the one of 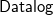 ${{\textsf{Datalog}}}$.
${{\textsf{Datalog}}}$.