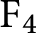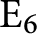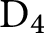We study exceptional Jordan algebras and related exceptional group schemes over commutative rings from a geometric point of view, using appropriate torsors to parametrize and explain classical and new constructions, and proving that over rings, they give rise to nonisomorphic structures.
We begin by showing that isotopes of Albert algebras are obtained as twists by a certain 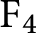 $\mathrm F_4$
-torsor with total space a group of type
$\mathrm F_4$
-torsor with total space a group of type 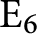 $\mathrm E_6$
and, using this, that Albert algebras over rings in general admit nonisomorphic isotopes even in the split case, as opposed to the situation over fields. We then consider certain
$\mathrm E_6$
and, using this, that Albert algebras over rings in general admit nonisomorphic isotopes even in the split case, as opposed to the situation over fields. We then consider certain 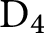 $\mathrm D_4$
-torsors constructed from reduced Albert algebras, and show how these give rise to a class of generalised reduced Albert algebras constructed from compositions of quadratic forms. Showing that this torsor is nontrivial, we conclude that the Albert algebra does not uniquely determine the underlying composition, even in the split case. In a similar vein, we show that a given reduced Albert algebra can admit two coordinate algebras which are nonisomorphic and have nonisometric quadratic forms, contrary, in a strong sense, to the case over fields, established by Albert and Jacobson.
$\mathrm D_4$
-torsors constructed from reduced Albert algebras, and show how these give rise to a class of generalised reduced Albert algebras constructed from compositions of quadratic forms. Showing that this torsor is nontrivial, we conclude that the Albert algebra does not uniquely determine the underlying composition, even in the split case. In a similar vein, we show that a given reduced Albert algebra can admit two coordinate algebras which are nonisomorphic and have nonisometric quadratic forms, contrary, in a strong sense, to the case over fields, established by Albert and Jacobson.