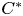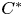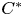1 results
Classification of irreversible and reversible Pimsner operator algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 13 January 2021, pp. 2510-2535
- Print publication:
- December 2020
-
- Article
- Export citation