We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that March’s criterion for the existence of a bounded nonconstant harmonic function on a weak model (that is,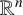 
$\mathbb {R}^n$ with a rotationally symmetric metric) is also a necessary and sufficient condition for the solvability of the Dirichlet problem at infinity on a family of metrics that generalise metrics with rotational symmetry on 
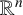$\mathbb {R}^n$. When the Dirichlet problem at infinity is not solvable, we prove some quantitative estimates on how fast a nonconstant harmonic function must grow.
