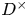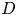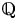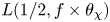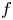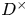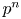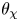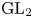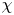5 results
Exponential mixing of frame flows for convex cocompact hyperbolic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 08 November 2021, pp. 2585-2634
- Print publication:
- December 2021
-
- Article
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
A Weak Formulation for Solving the Elliptic Interface Problems with Imperfect Contact
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1189-1205
- Print publication:
- October 2017
-
- Article
- Export citation
A Numerical Method for Solving Matrix Coefficient Heat Equations with Interfaces
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 475-495
- Print publication:
- November 2015
-
- Article
- Export citation
Matrix coefficients of cohomologically induced representations
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 1 / January 2007
- Published online by Cambridge University Press:
- 19 January 2007, pp. 201-221
- Print publication:
- January 2007
-
- Article
-
- You have access
- Export citation