We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this article, we propose a new classification of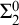 
$\Sigma ^0_2$ formulas under the realizability interpretation of many-one reducibility (i.e., Levin reducibility). For example, 
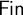$\mathsf {Fin}$, the decision of being eventually zero for sequences, is many-one/Levin complete among 
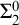$\Sigma ^0_2$ formulas of the form 
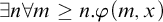$\exists n\forall m\geq n.\varphi (m,x)$, where 
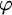$\varphi $ is decidable. The decision of boundedness for sequences 
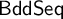$\mathsf {BddSeq}$ and for width of posets 
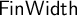$\mathsf {FinWidth}$ are many-one/Levin complete among 
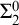$\Sigma ^0_2$ formulas of the form 
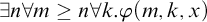$\exists n\forall m\geq n\forall k.\varphi (m,k,x)$, where 
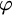$\varphi $ is decidable. However, unlike the classical many-one reducibility, none of the above is 
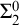$\Sigma ^0_2$-complete. The decision of non-density of linear orders 
$\mathsf {NonDense}$ is truly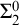 
$\Sigma ^0_2$-complete.
