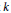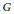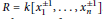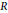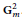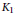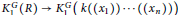Let 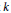k$k$ be a field of characteristic 0. Let 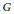G$G$ be a reductive group over the ring of Laurent polynomials 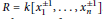R\,=\,k\left[ x_{1}^{\pm 1},\ldots ,x_{n}^{\pm 1} \right]$R\,=\,k\left[ x_{1}^{\pm 1},\ldots ,x_{n}^{\pm 1} \right]$ . Assume that 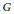G$G$ contains a maximal 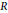R$R$ -torus, and that every semisimple normal subgroup of 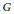G$G$ contains a two-dimensional split torus 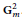\mathbf{G}_{m}^{2}$\mathbf{G}_{m}^{2}$ . We show that the natural map of non-stable 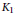{{K}_{1}}${{K}_{1}}$ -functors, also called Whitehead groups, 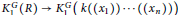K_{1}^{G}\left( R \right)\,\to \,K_{1}^{G}\left( k\left( \left( {{x}_{1}} \right) \right)\cdots \left( \left( {{x}_{n}} \right) \right) \right)$K_{1}^{G}\left( R \right)\,\to \,K_{1}^{G}\left( k\left( \left( {{x}_{1}} \right) \right)\cdots \left( \left( {{x}_{n}} \right) \right) \right)$ is injective, and an isomorphism if 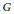G$G$ is semisimple. As an application, we provide a way to compute the difference between the full automorphism group of a Lie torus (in the sense of Yoshii–Neher) and the subgroup generated by exponential automorphisms.