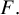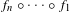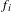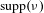2 results
A fixed-point curve theorem for finite-orbits local diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 February 2023, pp. 4138-4165
- Print publication:
- December 2023
-
- Article
- Export citation
Random local complex dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 2156-2182
- Print publication:
- August 2020
-
- Article
- Export citation