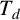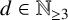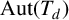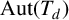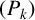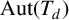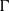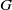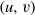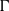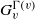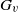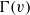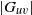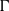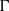We extend the Burger–Mozes theory of closed, nondiscrete, locally quasiprimitive automorphism groups of locally finite, connected graphs to the semiprimitive case, and develop a generalization of Burger–Mozes universal groups acting on the regular tree 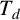$T_{d}$ of degree 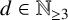$d\in \mathbb {N}_{\ge 3}$. Three applications are given. First, we characterize the automorphism types that the quasicentre of a nondiscrete subgroup of 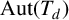$\operatorname {\mathrm {Aut}}(T_{d})$ may feature in terms of the group’s local action. In doing so, we explicitly construct closed, nondiscrete, compactly generated subgroups of 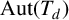$\operatorname {\mathrm {Aut}}(T_{d})$ with nontrivial quasicentre, and see that the Burger–Mozes theory does not extend further to the transitive case. We then characterize the 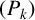$(P_{k})$-closures of locally transitive subgroups of 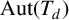$\operatorname {\mathrm {Aut}}(T_{d})$ containing an involutive inversion, and thereby partially answer two questions by Banks et al. [‘Simple groups of automorphisms of trees determined by their actions on finite subtrees’, J. Group Theory 18(2) (2015), 235–261]. Finally, we offer a new view on the Weiss conjecture.

Let $\Gamma $ be a $G$-vertex-transitive graph and let $(u,v)$ be an arc of $\Gamma $. It is known that if the local action $G_v^{\Gamma (v)}$ (the permutation group induced by $G_v$ on $\Gamma (v)$) is permutation isomorphic to the dihedral group of degree four, then either $|G_{uv}|$ is ‘small’ with respect to the order of $\Gamma $ or $\Gamma $is one of a family of well-understood graphs. In this paper, we generalise this result to a wider class of local actions.