We study the probability distribution of the location of a particleperforming a cyclic random motion in $\mathbb{R}^d$ 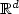 . The particle can taken possible directions with different velocities and the changes ofdirection occur at random times. The speed-vectors as well as thesupport of the distribution form a polyhedron (the first one havingconstant sides and the other expanding with time t). Thedistribution of the location of the particle is made up of twocomponents: a singular component (corresponding to the beginning ofthe travel of the particle) and an absolutely continuous component.
We completely describe the singular component and exhibit anintegral representation for the absolutely continuous one. Thedistribution is obtained by using a suitable expression of thelocation of the particle as well as some probability calculustogether with some linear algebra. The particular case of theminimal cyclic motion (n=d+1) with Erlangian switching times isalso investigated and the related distribution can be expressed interms of hyper-Bessel functions with several arguments.
. The particle can taken possible directions with different velocities and the changes ofdirection occur at random times. The speed-vectors as well as thesupport of the distribution form a polyhedron (the first one havingconstant sides and the other expanding with time t). Thedistribution of the location of the particle is made up of twocomponents: a singular component (corresponding to the beginning ofthe travel of the particle) and an absolutely continuous component.
We completely describe the singular component and exhibit anintegral representation for the absolutely continuous one. Thedistribution is obtained by using a suitable expression of thelocation of the particle as well as some probability calculustogether with some linear algebra. The particular case of theminimal cyclic motion (n=d+1) with Erlangian switching times isalso investigated and the related distribution can be expressed interms of hyper-Bessel functions with several arguments.
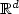 -space withn directions
-space withn directions