1 results
Least Energy Nodal Solutions for a Defocusing Schrödinger Equation with Supercritical Exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 August 2018, pp. 1-23
-
- Article
- Export citation
-
In this paper we consider the existence of least energy nodal solution for the defocusing quasilinear Schrödinger equation
where λ≥0 is a real parameter, V(x) is a non-vanishing function, a(x) can be a vanishing positive function at infinity, the nonlinearity g(u) is of subcritical growth, the exponent p≥22*, and N≥3. The proof is based on a dual argument on Nehari manifold by employing a deformation argument and an
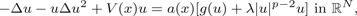$$-\Delta u - u \Delta u^2 + V(x)u = a(x)[g(u) + \lambda \vert u \vert ^{p-2}u] \hbox{in} {\open R}^N,$$
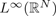$L</italic>^{\infty}({\open R}^{N})$-estimative.
