In this work, we obtain the pointwise almost everywhere convergence for two families of multilinear operators: (a) the doubly truncated homogeneous singular integral operators associated with 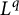 $L^q$ functions on the sphere and (b) lacunary multiplier operators of limited smoothness. The a.e. convergence is deduced from the
$L^q$ functions on the sphere and (b) lacunary multiplier operators of limited smoothness. The a.e. convergence is deduced from the 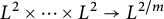 $L^2\times \cdots \times L^2\to L^{2/m}$ boundedness of the associated maximal multilinear operators.
$L^2\times \cdots \times L^2\to L^{2/m}$ boundedness of the associated maximal multilinear operators.