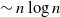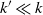1 results
Randomized near-neighbor graphs, giant components and applications in data science
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 458-476
- Print publication:
- June 2020
-
- Article
- Export citation