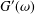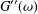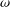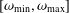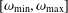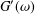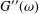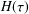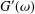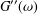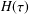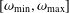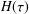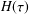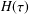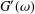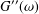In oscillatory shear experiments, the values of the storage and loss moduli, 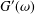G^{\prime }(\unicode[STIX]{x1D714})$G^{\pr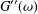ime }(\unicode[STIX]{x1D714})$ and G^{\prime \prime }(\unicode[STIX]{x1D714})$G^{\prime \prime }(\unicode[STIX]{x1D714})$, respectively, are only measured and recorded for a number of values of the frequency 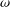\unicode[STIX]{x1D714}$\unicode[STIX]{x1D714}$ in some well-defined finite range 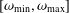[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$. In many practical situations, when the range 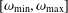[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$ is sufficiently large, information about the associated polymer dynamics can be assessed by simply comparing the interrelationship between the frequency dependence of 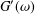G^{\prime }(\unicode[STIX]{x1D714})$G^{\pr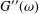ime }(\unicode[STIX]{x1D714})$ and G^{\prime \prime }(\unicode[STIX]{x1D714})$G^{\prime \prime }(\unicode[STIX]{x1D714})$. For other situations, the required rheological insight can only be obtained once explicit knowledge about the structure of the relaxation time spectrum 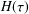H(\unicode[STIX]{x1D70F})$H(\unicode[STIX]{x1D70F})$ has been determined through the inversion of the measured storage and loss moduli 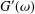G^{\prime }(\unicode[STIX]{x1D714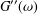})$G^{\prime }(\unicode[STIX]{x1D714})$ and G^{\prime \prime }(\unicode[STIX]{x1D714})$G^{\prime \prime }(\unicode[STIX]{x1D714})$. For the recovery of an approximation to 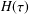H(\unicode[STIX]{x1D70F})$H(\unicode[STIX]{x1D70F})$, in order to cope with the limited range 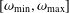[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$[\unicode[STIX]{x1D714}_{\text{min}},\unicode[STIX]{x1D714}_{\text{max}}]$ of the measurements, some form of localization algorithm is required. A popular strategy for achieving this is to assume that 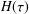H(\unicode[STIX]{x1D70F})$H(\unicode[STIX]{x1D70F})$ has a separated discrete point mass (Dirac delta function) structure. However, this expedient overlooks the potential information contained in the structure of a possibly continuous 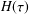H(\unicode[STIX]{x1D70F})$H(\unicode[STIX]{x1D70F})$. 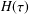In this paper, simple localization algorithms and, in particular, a joint inversion least squares procedure, are proposed for the rapid recovery of accurate approximations to continuous H(\unicode[STIX]{x1D70F})$H(\unicode[STIX]{x1D70F})$ from limited measurements of 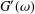G^{\prime }(\unicode[STIX]{x1D714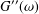})$G^{\prime }(\unicode[STIX]{x1D714})$ and G^{\prime \prime }(\unicode[STIX]{x1D714})$G^{\prime \prime }(\unicode[STIX]{x1D714})$.