We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove that, in the choiceless Solovay model, every set of reals is H-Ramsey for every happy family H that also belongs to the Solovay model. This gives a new proof of Törnquist’s recent theorem that there are no infinite mad families in the Solovay model. We also investigate happy families and mad families under determinacy, applying a generic absoluteness result to prove that there are no infinite mad families under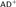 
$A{D^ + }$.
