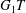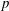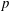1 results
Loewy series of parabolically induced
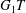 $G_1T$-Verma modules
$G_1T$-Verma modules
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 March 2014, pp. 185-220
- Print publication:
- January 2015
-
- Article
- Export citation